Сообщений 0    Оценка 500        Оценить

Код Грея

Автор: Холодилов Сергей Александрович

Опубликовано: 23.08.2010
Исправлено: 10.12.2016
Версия текста: 1.1

Затем мы отправимся, но куда - не скажу; во всяком случае, недалеко отсюда.
Я еду к жене. Она еще не жена мне, но будет ею. Мне нужны алые паруса, чтобы
 еще издали, как условлено с нею, она заметила нас. Вот и все. Как видите, 
здесь нет ничего таинственного. И довольно об этом. 

Александр Грин, «Алые паруса»

Представьте себе, что вы – молодой капитан Грей, уже знающий, что Ассоль сидит на берегу, смотрит вдаль и ждёт. Ушибленный на голову волшебник обещал ей принца, использующего такое двоичное представление чисел, что коды соседних чисел отличаются ровно на один бит.

Чего не сделаешь ради счастья любимой женщины, приходится придумывать. В каких ещё ситуациях такое кодирование может оказаться полезным – посмотрим в конце.

Наложим несколько ограничений:

• Было бы здорово, если бы, имея n битов, мы могли бы закодировать все числа от 0 до 2ⁿ-1. Т.е. если у нас 8 бит, а код числа 5 ну ни как не влезает, это плохо. Даже если ни одна комбинация не пропадает, и какой-то 8-и битной соответствует число 1567 – всё равно плохо. Очень неудобно с практической точки зрения.
• При этом код числа не должен зависеть от того, сколько битов у нас есть. Ситуации, когда при 8-и доступных битах код числа 5 требует 6 битов, а при 32-х – 17, хотелось бы избежать. Чтобы не приходилась каждый раз оговаривать, сколько битов есть. Пусть 5 всегда будет 5.

Кодировку, удовлетворяющую этим ограничениям, назовём вменяемой (это же математика! тут нельзя без строгой терминологии). Очевидное необходимое и достаточное условие вменяемости:

• Код числа, меньшего 2ⁿ должен занимать не более чем n битов.

Отсюда сразу получаем:

• код 0 – 0000 (для него должно хватать 0 бит, ага)
• код 1 – 0001
• код 2 – 0011 (а как ещё изменить только 1 бит, остаться в пределах 2-х битов, и не повториться?)
• код 3 – 0010
• код 4 – 0110

А вот дальше могут быть варианты. А жаль, а то бы сразу раз – и всё построили.

Разработка

Раз сразу не получилось, попробуем подумать:

• Коды чисел до 2ⁿ-1 влезают в n бит (это из требования вменяемости).
• Более того, так как таких чисел слолько же, сколько кодов длины не более n, они не просто влезают, у них взаимнооднозначное соответствие. Т.е. после числа 2ⁿ-1 свободных комбинаций из первых n битов уже не осталось.
• Коды чисел до 2ⁿ⁺¹-1 влезают в n+1 бит (по вменяемости).
• Коды чисел от 2ⁿ до 2ⁿ⁺¹-1 не могут влезать в n бит, т.к. там уже всё разобрано. Значит у них всех n-й бит установлен в 1 (биты нумеруются с 0).
• Рассмотрим код числа 2ⁿ. Его n-й бит равен 1. При этом отличается от кода 2ⁿ-1 только одним битом. Значит вот этим n-м битом и отличается, остальные совпадают.

Получили следующую схему:

Теперь предположим, что мы добрались до 2ⁿ и надо двигаться дальше – к 2ⁿ⁺¹.

• Коды чисел до 2ⁿ⁺¹-1 влезают в n+1 бит
• При этом у кодов всех чисел от 2ⁿ до 2ⁿ⁺¹-1 n-й бит равен 1.
• Таких кодов 2ⁿ штук; для того, чтобы они все отличались, нам нужно перебрать все комбинации значений младших n битов.
• Младшие n бит кода числа 2ⁿ совпадают с кодом числа 2ⁿ-1

Итого: нужно перебрать все комбинации из n битов, так, чтобы первой был код 2ⁿ-1, и каждые две соседние отличались бы ровно одним битом.

Вариантов такого перебора много, но среди них есть один красивый. Дело в том, что у нас уже есть подходящая последовательность: коды чисел от 0 до 2ⁿ-1. Если взять её в обратном порядке, получится ровно то, что нужно.

Это и есть код Грея.

Понятное объяснение

Начнём с первых двух чисел, закодируем их нулём и единицей:

Ноль       0
Один       1

Заметим, что они отличаются только одним битом. Проблема в том, что нам нужно больше чем два числа. Зеркально отразим коды чисел:

Ноль       0
Один       1
          --  - ось симметрии
           1
           0

Кодов стало больше, и соседи отличаются друг от друга не более чем одним битом. Но есть повторы. Чтобы не было повторов, допишем спереди к первой половине кодов 0, а ко второй 1.

Ноль      00
Один      01
         ---
Два       11
Три       10

Точно так же мы можем отразить и их

Ноль      00
Один      01
Два       11
Три       10
         ---
          10
          11 
          01
          00

И тоже добавим в первую половину 0, а во вторую – 1.

Ноль     000
Один     001
Два      011
Три      010
        ----
Четыре   110
Пять     111
Шесть    101
Семь     100

И т.п.

В общем виде

Должно быть уже понятно, но на всякий случай:

Историческая справка

Именно в таком виде этот код был предложен инженером Bell Labs Фрэнком Греем (Frank Gray) в 1947-м году. Код описан в патенте 2632058 (оформлен в 1953-м), и подраздел «Понятное объяснение» целиком стянут оттуда (вслед за [Doran 07]). Первоначально Грей предложил название «reflected binary code», но очень быстро на него начали ссылаться просто как на «код Грея».

С предысторией несколько сложнее.

В 1870-x годах французский инженер Эмиль Бодо (Émile Baudot) занимался усовершенствованием телеграфа; в 1878-м году его телеграф получил золотую медаль на Всемирной выставке в Париже, после чего быстро распространился по миру. В то время телеграфы в основном передавали морзянку, основное отличие телеграфа Бодо было в том, что он печатал буквы. Конечно, для этого ему потребовался двоичный код фиксированной длины.

Разрабатывая код, Бодо боролся с нечеловеческим интерфейсом ввода данных. Клавиатура его телеграфа состояла из пяти клавиш, каждая из которых отвечала за один бит, коды символов вводились вручную (и при этом нужно было выдерживать правильный темп!). Бодо стремился минимизировать количество переключений и этим упростить работу оператора.

Скорее всего, он проанализировал частотность биграмм и поместил на «соседние» кодовые позиции часто встречающиеся рядом буквы. Но код Грея даёт только две соседние позиции (следующее и предыдущее слово). А для слова из пяти бит их, конечно, пять, и жалко терять остальные.

Дальше есть два варианта:

• Честно придумать оптимальное кодирование. После чего расставить элементы как-нибудь красиво.
• Оператор работает двумя руками: две клавиши для левой и три для правой. Если рассматривать и кодировать эти части отдельно, получаем четыре соседних кодовых слова. Четыре это почти пять, пятую при желании можно учесть отдельно.

Картинки, на которых код Бодо похож на код Грея, выглядят специфически: по горизонтали отложены четыре варианта положения клавиш левой руки, по вертикали – восемь вариантов положения правой, на пересечениях находятся символы. Положения клавиш приведены в порядке кода Грея.

В 1901-м году Дональд Мюррей (Donald Murray) сделал нормальную клавиатуру для телеграфа, и заодно переработал код.

Генерация последовательности

Действуем по определению. Возрастающая последовательность n-битных кодов строится из последовательности (n-1)-битных следующим образом:

• дописать спереди 0 к возрастающей (n-1)-битной последовательности
• дописать спереди 1 к убывающей (n-1)-битной последовательности (тогда зеркально получается)

Если читать это в обратном порядке, получится, естественно, убывающая n-битная последовательность. Соответственно, она строится аналогично, изменится только старший разряд:

• дописать спереди 1 к возрастающей (n-1)-битной последовательности (была убывающая, но если читать наоборот...)
• дописать спереди 0 к убывающей (n-1)-битной последовательности

Реализация:

      # n - ширина в битах
      # d - направление. 0 -- вверх, 1 -- вниз. 
def generate(n, d = 0):
    if n == 0:
        return [[]]
    if d == 0:
        # возрастающая 
        return [[0] + x for x in generate(n-1, 0)] # первая половина
             + [[1] + x for x in generate(n-1, 1)] # вторая половина
    else:
        # убывающая
        return [[1] + x for x in generate(n-1, 0)]
             + [[0] + x for x in generate(n-1, 1)]

Или, то же самое, чуть более изящно (заметим закономерность, связывающую значения d и значения n-ного разряда):

def generate(n, d = 0):
    if n == 0:
        return [[]]
    return [[d]   + x for x in generate(n-1, 0)] 
         + [[1-d] + x for x in generate(n-1, 1)]

На С++:

      // Возвращает value с n-ым битом, установленным в b
      int setBit(int value, int n, int b)
{
    return (value & ~(1 << n)) | (b << n);
}

// [in]  n - количество бит// [in]  d - направление, 0 -- возрастает, 1 -- убывает// [out] result - массив с результатами. Длинна должна быть не меньше чем 2**n// Возвращает: количество сгенерированных чиселint generateGray(int n, int d, int* result)
{
    if (n == 0) return 1;

    // Получаем возрастающую последовательностьint firstHalf = generateGray(n - 1, 0, result);

    for (int i = 0; i < firstHalf; i++)
    {
        // Устанавливает n-й бит (биты нумеруются с 0!) в d
        result[i] = setBit(result[i], n - 1, d);
    }

    // Получаем убывающую последовательностьint secondHalf = generateGray(n - 1, 1, result + firstHalf);

    for (int i = 0; i < secondHalf; i++)
    {
        // Устанавливает n-й бит в (d-1)
        result[firstHalf + i] = setBit(result[firstHalf + i], n - 1, 1 - d);
    }

    return firstHalf + secondHalf;
}

Кодирование значения

Во-первых, это тоже можно сделать по определению. Идея очень простая:

• Как видно из генерируемой последовательности, если v < 2ⁿ, то n-й бит v равен 0
• Если мы нашли старший единичный бит, то что такое младшие биты? По построению, это код Грея некоторого n-1 битного числа.
• И, вспомнив построение, несложно понять, какого

Код:

      # n -- значение
      # b -- разрядность
def encode2Gray1(value, n):
    if n == 0:
        return 0   
    highBit = (1 << (n - 1))
    if value < highBit:
        return encode2Gray1(value, n - 1)
    # столько шагов нужно будет сделать вниз по убывающей последовательности
    rest = value - highBit 
    # А это то же самое, что сделать highBit - 1 - rest шагов по возрастающей
    return highBit + encode2Gray1(highBit - 1 - rest, n - 1)

Но есть другой вариант. Давайте займёмся странными исследованиями и найдём неожиданную закономерность. Исследования следующие: вместе с кодом Грея будем генерировать обычный двоичный код. Ну, просто так, вдруг чего обнаружим.

      # Возвращает список пар, первый элемент пары -- двоичный код, второй -- код Грея
def generateGB(n, d = 0):
    if n == 0:
        return [([], [])]
    
    # Явно выпишем половинки и значения битов на текущем этапе
    bn0 = 0
    gn0 = d
    res0 = generateGB(n-1, 0)

    bn1 = 1    
    gn1 = 1-d
    res1 = generateGB(n-1, 1)
    
    return [ ([bn0] + x, [gn0] + y) for x,y in res0] 
         + [ ([bn1] + x, [gn1] + y) for x,y in res1]

Отметим следующие замечательные факты:

• Передаваемое дальше значение d совпадает с соответствующим bn_i
• Это значение определяет значения следующих разрядов gn_i

Середину функции можно переписать так:

    ...
    bn0 = 0
    gn0 = d ^ bn0   # т.к. это равно d
    res0 = generateGB(n-1, bn0)

    bn1 = 1    
    gn1 = d ^ bn1   # a это равно 1-d
    res1 = generateGB(n-1, bn1)
    ...

С учётом того, что d это предыдущий (старший) разряд двоичного кода, получаем, что g[i] = b[i+1] ^ b[i]. И очевидную функцию кодирования:

def encode2Gray2(b):
    return b ^ (b >> 1)

Результат не очевидный, есть ощущение, что он получен каким-то трюком, и хорошо ещё, если обошлось без жульничества. Попробуем обосновать.

Обоснование равносильности

Способ вычисления кода Грея g = b ^ (b >> 1) со всех сторон замечателен, но пока непонятно, почему у соседей будет отличаться только один бит, и почему вся эта конструкция будет симметрична, т.е. похожа на наш, "всамделишный" код Грея.

Соседи

Пусть b = b[n] .. b[k] | 01..1

Тогда b+1 = b[n] .. b[k] | 10..0. Запишем в столбик.

g0 = b ^ (b >> 1):

g1 = (b+1) ^ ((b+1) >> 1):

Видно, что изменился ровно один разряд. И даже видно, какой именно – запомните, дальше пригодится.

Симметричность

По построению кода Грея, должно выполняться равенство gray(2ⁿ + x) = 1 | gray(2ⁿ - 1 - x). Проверим.

g0 = (2ⁿ + x) ^ ((2ⁿ + x) >> 1):

С учётом того, что 2ⁿ – 1 – x это инвертированное x, g1 = (2ⁿ - 1 - x) ^ ((2ⁿ - 1 - x) >> 1):

Сравниваем:

• Старшие биты отличаются
• x[n-1] ^ 1 = !x[n-1] = !x[n-1] ^ 0, значит n-1-е биты совпадают.
• a ^ b = !a ^ !b, значит все остальные биты тоже совпадают.

Что и требовалось доказать.

.. и всё же

Доказать доказали, но понятнее, почему это одно и тоже от этого не стало.

Равенство g[i] = b[i+1] ^ b[i] равносильно равенству g[i] = (b[i+1] != b[i]). То есть, в коде Грея единичка будет в том месте, где в обычном двоичном коде был переход 0-1 или 1-0 (включая первый переход, из 0 в старший единичный разряд). Например, так:

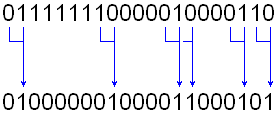
Рис. 1. Преобразование из обычного двоичного кода в код Грея

А теперь помедитируйте над абзацем, описывающим работу функции encode2Gray1:

То есть, при кодировании в код Грея, каждый раз, когда мы получаем 1, мы инвертируем остаток кодируемого числа. На следующем шаге берём его старший бит и так далее.

.. и осознайте, что это в точности то же самое.

Таким образом, взаимосвязь между двумя способами кодирования будем считать прояснённой. Это не случайность и не трюк.

Декодирование

Тоже можно сделать по определению, и тоже понятно как:

• Воспользуемся полученным выше результатом: gray(2ⁿ + x) = 1 | gray(2ⁿ - 1 - x)
• Это он же: gray(1 | binary(x)) = 1 | gray(2ⁿ - 1 - x). Значит, старший бит понятно, как получить.
• Функция degray(gray(2ⁿ - 1 - x)) вернёт, конечно, 2ⁿ - 1 - x
• Значит x = 2ⁿ - 1 - degray(gray(2ⁿ - 1 - x))

Код:

def decodeFromGray1(value, n):
    if n == 0:
        return 0
    highBit = (1 << (n - 1))
    if value < highBit:
        return decodeFromGray1(value, n - 1)
    return highBit + (highBit - 1 - decodeFromGray1(value - highBit, n - 1))

Другой вариант декодирования получается из g[i] = b[i+1] ^ b[i]. Из него сразу же следует b[i] = g[i] ^ b[i+1]. Ну и:

      
b[n] = 0
b[n-1] = g[n-1] ^ b[n] = g[n-1]
b[n-2] = g[n-2] ^ b[n-1] = g[n-2] ^ g[n-1]
b[n-3] = g[n-3] ^ b[n-2] = g[n-3] ^ g[n-2] ^ g[n-1]
...
b[n-i] = g[n-i] ^ g[n-i+1] ^ ... ^ g[n-1]
...

А реализовать это проще всего так:

def decodeFromGray2(value, n):
    res = value
    for i in range(1, n):
        res ^= (value >> i)
    return res

+1

Задача получить следующий элемент кода, имея текущий, приходит в голову сразу. Пока что было два варианта решения: либо сгенерировать сразу серию, либо перекодировать в двоичный код, прибавить в единицу, и перекодировать обратно в код Грея. Оба варианта не очень красивые. Попробуем придумать алгоритм для честного прибавления единицы в коде Грея.

Из того, что в коде Грея единицы соответствуют переключениям 0-1 и 1-0 в обычном двоичном коде, получаем, что пары единиц кода Грея задают диапазоны единиц в двоичном коде.

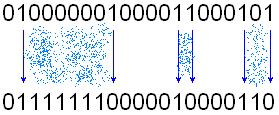
Рис. 2. Преобразование из кода Грея в двоичный.

Что сразу видно:

• «Нечётные» единицы в коде Грея (если считать начиная со старшей) соответствуют началу диапазона единиц в двоичном коде, «чётные» – окончанию.
• Если в коде Грея нечётное количество единиц, последний диапазон единиц в двоичном коде продолжается до конца числа. Т.е. младший разряд двоичного кода – 1. Т.е. число нечётное.
• И наоборот, если в коде Грея чётное количество единиц, число чётное.

Посмотрим, что будет, если прибавить 1.

Чётные

Итак, младший разряд двоичного кода – 0, и после прибавления единицы он должен стать 1. Но всё равно есть два случая: эта единица может быть отдельно стоящей или она вольётся в ряд таких же единиц.

Обе ситуации изображены на рисунках 3 и 4. В верхней строчке – двоичный код, в нижней – код Грея, единички в коде Грея соответствуют переходам 0-1 и 1-0 в двоичном коде. Изменяющийся бит подчёркнут.

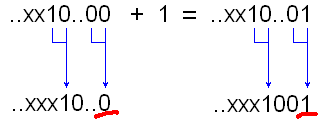
Рис.3. Прибавление 1 к четному числу, версия 1

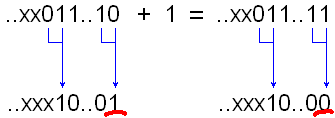
Рис.4. Прибавление 1 к четному числу, версия 2

Видно, что в обоих случаях для получения кода Грея числа, большего на 1, нужно просто инвертировать младший бит.

Нечётные

Тоже два случая, по тому же признаку: будет новая единица в отдельной группе, или присоединится к какой-то из существующих.

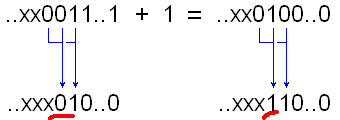
Рис.5. Прибавление 1 к нечётному числу, версия 1.

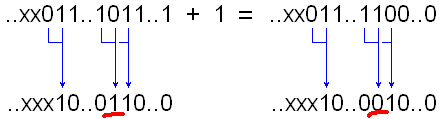
Рис.6. Прибавление 1 к нечётному числу, версия 2.

И в том и в другом случае нужно инвертировать бит, следующий за первой единицей.

Вместе

Реализация очевидна

        # Самая простая реализация проверки на чётность количества единичных битов
def isGrayEven(n):
    count = 0
    while n:
        if n & 1: count += 1
        n >>= 1
    return (count % 2 == 0)

# Возвращает число, в котором в 1 установлен только один бит,# тот самый, который был младшим единичным в n 
def getLesserOne(n):
    return n & ~(n-1) # почему это работает как надо? :)# Возвращает код Грея, следующий за n
def getNextGray(n):
    if isGrayEven(n):
        return n ^ 1
    return n ^ (getLesserOne(n) << 1)

Если немного подумать, можно написать функцию getPrevGray.

+много

Сложение чисел в коде Грея по возможной области применимости резко выделяется на фоне остальной части статьи: это уже не просто никому не нужно, это вообще никому не нужно. У самого кода Грея всё же есть разумные применения, но ни одно из известных мне не предполагает суммирования кодовых комбинаций. Но человеческий разум не знает преград.

Пусть A, B, S – слагаемые и сумма в бинарном коде, а A_g, B_g, S_g – в коде Грея.

Идея алгоритма:

• Заметим, что S_g[i] = S[i+1] ^ S[i]
• При этом S[i] = A[i] ^ B[i] ^ C[i-1], где C[i-1] – перенос из предыдущего разряда.
• Подставляем, получаем: S_g[i] = (A[i+1] ^ B[i+1] ^ C[i]) ^ (A[i] ^ B[i] ^ C[i-1])
• Перегруппируем: S_g[i] = (A[i+1] ^ A[i]) ^ (B[i+1] ^ B[i]) ^ (C[i] ^ C[i-1])
• Заметим, что A[i+1] ^ A[i] = A_g[i], а B[i+1] ^ B[i] = B_g[i]
• Значит S_g[i] = A_g[i] ^ B_g[i] ^ (C[i] ^ C[i-1])

Осталось красиво выразить C[i] ^ C[i-1]. Обозначим это выражение за C_g[i] и через пару строчек выкладок получим, что C_g[i] = (A[i] ^ C[i-1]) & (B[i] ^ C[i-1]). Теперь нужно вспомнить, что

• A[i] = A[i-1] ^ A_g[i-1]
• C[i] = C[i-1] ^ C_g[i]

То есть C_g[i] это конъюнкция двух выражений, которые несложно вычислять рекурсивно на каждом шаге. Ну и нужно как-то начать, и это тоже несложно. Итого, шаг алгоритма:

• S_g[i] = A_g[i] ^ B_g[i] ^ E[i] & F[i]
• E[i+1] = E[i] ^ A_g[i] ^ E[i] & F[i]
• F[i+1] = F[i] ^ B_g[i] ^ E[i] & F[i]

Где E[i] и F[i] это части C_g[i].

Ещё о вычислении значения

Посмотрим, что такое «диапазоны единиц».

• Полоса единичных битов от разряда m до младшего разряда это число (2^m+1-1)
• Полоса единичных битов между разрядами m и k задаётся разностью (2^m+1-1) – (2^k+1-1).

Итоговое значение это просто сумма всех получившихся «полос». То есть, если t₁,..t_m – номера битов, равных 1 в коде Грея, и t₁ < t₂ < .. < t_m, то при преобразовании в двоичный код мы получим:

(2^t[m]+1-1) – (2^t[m-1]+1-1) + (2^t[m-2]+1-1) – (2^t[m-3]+1-1) + … + (2^t[2]+1-1) – (2^t[1]+1-1)

если m – чётное и

(2^t[m]+1-1) – (2^t[m-1]+1-1) + (2^t[m-2]+1-1) – (2^t[m-3]+1-1) + … + (2^t[3]+1-1) – (2^t[2]+1-1) + (2^t[1]+1-1)

в противном случае.

Пусть P(a₁..a_k) равно 0, если среди битов a₁..a_k чётное количество единичных и 1, если их нечётное. Тогда оба эти выражения можно свести в одно. Следующая последовательность преобразований:

• Заметим, что плюс или минус перед (2ⁱ⁺¹-1) определяется тем, чётное число единичек было до него, или нет. Т.е. значением P(g_n-1..g_i+1). Даже можно так: (-1)^{P(g[n-1]..g[i+1])}.
• Заметим, что, умножив слагаемые на значения соответствующих битов, мы ничего не изменим, т.к. все эти биты как раз равны 1.
• А умножать на значения остальных битов можно любой мусор, так как они все равны 0.

Приводит к:

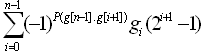
То есть, по существу от обычной позиционной системы счисления результат отличается только множителем (-1)^{P(g[n-1]..g[i+1])}, из-за которого значение разряда не постоянно, а зависит от количества старших единичных разрядов.

Обобщения

Кодом Грея «в широком смысле» называют любой код, в котором соседние значения отличаются только в одном разряде, а значения этого разряда отличаются на 1.

Есть два разумных направления для обобщений:

• Переход от двоичной системы к какой-нибудь другой.
• Переход от зеркального кода к какому-то другому. При этом (обычно) речь идёт о коде с некоторой конкретной разрядностью. И, даже если он некоторым образом рекурсивно строится из кода меньшей разрядности, он совсем не обязательно является его продолжением. То есть, код числа 5 в кодах разной разрядности может сильно отличаться.

По первому вопросу сказать толком нечего. По второму, в общем, тоже. У обобщенного понятия остаётся слишком мало интересных свойств, а разбор конкретных воплощений – дело отдельных статей. Но общий подход ко всем таким кодам стоит упомянуть.

n-мерный куб

n-битное число можно рассматривать как вектор в n-мерном пространстве, каждый бит – координата по соответствующей оси. Все точки с координатами из нулей и единиц это вершины единичного n-мерного кубика, стоящего в начале координат. И все его вершины – это как раз такие точки. У двух соседних вершин отличается ровно одна из координат – по соединяющему их ребру.

Значит, если мы построим путь по рёбрам такого куба, мы получим код, в котором соседние значения отличаются не более чем на один бит. И наоборот, каждому такому коду соответствует путь в n-мерном кубе.

В теории графов путь, проходящий по одному разу через каждую вершину графа, называют Гамильтоновым путём. А если в конце он возвращается в исходную вершину, то это Гамильтонов цикл. Гамильтонову циклу соответствует код, который можно замкнуть и правило «не более одного бита» не нарушиться; т.е. последний элемент отличается от первого на один бит. Такой код называется циклическим. Несложно заметить, что классический код Грея – циклический.

Применение

Патент Фрэнка Грея посвящён преобразователю аналогового сигнала в цифровой. Преобразователь устроен следующим образом:

• Есть электронная пушка, она молотит по аноду, между пушкой и анодом – экран.
• Измеряемое напряжение отклоняет луч по вертикали. Т.е. задаёт строчку.
• Под действием периодического напряжения луч постоянно пробегает по строке.
• На экран нанесена маска с кодом. Прозрачные участки соответствуют единицам, непрозрачные – нулям. Соответственно, в строках находятся коды значений.
• При проходе через прозрачный участок, электронный луч вызывает импульс на аноде.

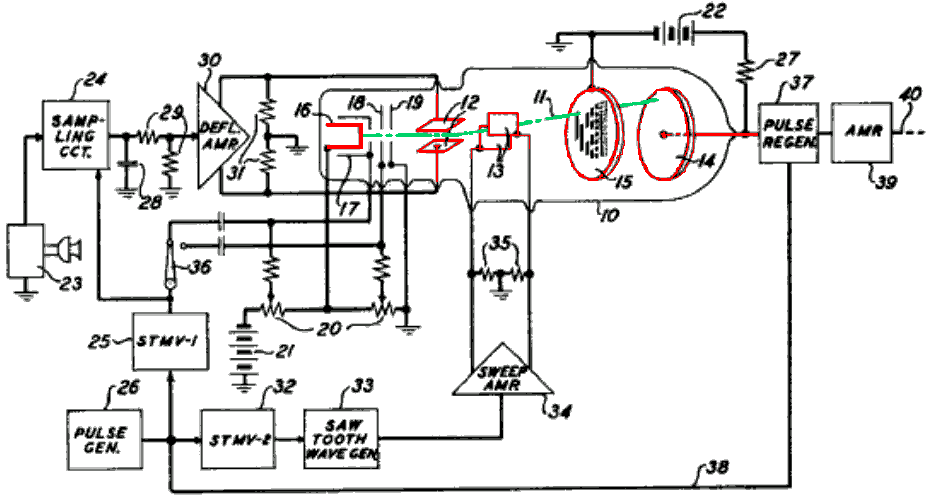
Рис.7. Преобразователь, описанные части схемы выделены красным, луч электронов зелёным (картинка взята из [Gray 53]).

Это все придумал не Грей, это было до него. Грей придумал, как победить основную проблему этого преобразователя: если луч оказывается около границы двух строк, до анода доходит случайная смесь из первой и второй строки. Так как в обычном двоичном коде соседние строки могут отличаться довольно сильно, погрешность получается большой. Идея Грея была в том, что если строки отличаются только одним битом, то, как ни смешивай, дойдёт либо одна, либо вторая.

Та же мысль применяется, например, в датчиках угла поворота.

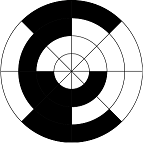
Рис.8. Круговой энкодер с трёхбитным кодом Грея (картинка взята из википедии, спасибо им)

Но здесь оказывается важным ещё и то, что разница между первым и последним кодом тоже 1 бит, т.е. то, что код Грея циклический.

В других областях коды Грея могут использоваться, если нужно перебрать все варианты чего-либо, и то, что соседние варианты отличаются мало, позволяет сократить вычисления (использовать результаты вычислений над предыдущим вариантом, чуть-чуть изменив их, а не вычислять всё заново). В [Guan 96] этот подход использован для подбора коэффициентов полинома кода коррекции ошибок. Автор утверждает, что помогло.

Список литературы

• [Doran 07] Robert W. Doran The Gray Code, Journal of Universal Computer Science, vol. 13, no. 11 (2007). Всеобъемлющая статья по теме, 25 страниц, 51 ссылка.
• [Gray 53] Frank Gray Pulse code communication, 1953. Патент №2632058
• [Guan 96] Dah-Jyh Guan Generalized Gray Codes with Applications, Proc. Natl. Sci. Counc. ROC(A) Vol. 22, No. 6, 1998.
• [Lucal 59] Harold M. Lucal «Arithmetic operations for digital computers using a modified reflected binary code», IEEE Transactions on Computers, vol. 8, no. 4, 1959.

Сообщений 0    Оценка 500        Оценить